Macro Musings

This week I was a guest on David Beckworth’s Macro Musings podcast. We discussed my policy brief on the labor standard as well as monetary policy more generally. Here is a link for those interested.

Updates

A couple of updates:

• The topic of this month’s Cato Unbound is J.P. Koning’s proposal for the U.S. to issue a large denomination “supernote” and to tax that note as a way of punishing illegal activity. I will be contributing to the discussion this month along with James McAndrews and Will Luther. You can read J.P.’s lead essay here. The response essays will be linked below the lead essay. My response essay will appear next week.
• My paper with Alex Salter and Brian Albrecht entitled “Preventing Plunder: Military Technology, Capital Accumulation, and Economic Growth” has been accepted at the Journal of Macroeconomics. I think that this paper is based on a really interesting idea (biased, I know). The basic idea is that military technology is a limiting factor for economic growth. We also suggest that both economic growth (at least to some degree) and state capacity could be driven by this common factor.

Monetary Policy as a Jobs Guarantee

Today, the Mercatus Center published my policy brief on the idea of a “labor standard” for monetary policy that was first proposed by Earl Thompson and David Glasner.

How Did the Gold Standard Work? Part 1: The Efficiency of the Gold Standard

Sebastian Edwards has written an interesting new book about FDR’s devaluation of the dollar and the legal and economic consequences thereof. This post is not about the book, although I do recommend it. What I would like to write about is motivated by some of the reaction to this book that I’ve seen and heard regarding gold and the gold standard. In recent years, I have become convinced that what I thought was the conventional wisdom on the gold standard is not widely understood. So I’d like to write a series of posts on the gold standard and how it worked. My tentative plan is as follows:

Part 1. The efficiency of the gold standard.
Part 2. The determination of the price level under the gold standard.
Part 3. The Monetary Approach to the Balance of Payments vs. the Price-Specie Flow Mechanism
Part 4. Gold standard interpretations of the Great Depression.

I don’t have a timeline for when these will be posted, but it is my hope to have them posted in a timely fashion so that they can get the appropriate readership. With that being said, let’s get started with Part 1: The efficiency of the gold standard.

Some people define the gold standard in their own particular way. I want to use as broad of a definition as possible. So I will define the gold standard as any monetary system in which the unit of account (e.g. the dollar) is defined as a particular quantity of gold. This definition is broad enough to encapsulate a wide variety of monetary systems, including but not limited to free banking and the pre-war international gold standard. Given this definition, the crucial point is that when the unit of account is defined as a particular quantity of gold, this implies that gold has a particular price in terms of this unit of account. In other words, if the unit of account is the dollar, then all prices are quoted in terms of dollars. The price of gold is no different. However, since the dollar is defined as a particular quantity of gold, this implies that the price of gold is fixed. For example, if the dollar is defined as 1/20 of an ounce of gold, then the price of an ounce of gold is $20.

This type of characteristic poses a lot of questions. Does the market accept this price? Or, is there any tendency for the market price of gold to equal the official, or mint price? This is a question of efficiency. If the market price of gold differs substantially from the official price, then the gold standard cannot be thought of as efficient and one must consider the implications thereof for the monetary system. What determines the price level under this sort of system? Does the quantity theory of money hold? What about purchasing power parity? In many ways, these questions are central to understanding not only of how the gold standard worked, but also the nature of business cycles under a gold standard. The price level and purchasing power parity arguments are equilibrium-based arguments. This raises the question as to what mechanisms push us in the direction of equilibrium. We therefore need to compare and contrast the monetary approach to the balance of payments with the price-specie flow mechanism. Finally, given this understanding, I will use the answers of this question to gain some insight into the role of the gold standard with regards to the Great Depression.

In terms of efficiency, we can think about the efficiency of the gold market in one of two ways. We could consider the case in which the dollar is the only currency defined in terms of gold. In this case, the U.S. would have an official price of gold, but gold would be sold in international markets and the price of gold in terms of foreign currencies is entirely market-determined. Alternatively, we could consider the case of an international gold standard in which many foreign currencies are defined as a particular quantity of gold. For simplicity, I will use the latter assumption.

This first post is concerned with whether or not the gold standard was efficient. So let’s consider the conditions under which the gold standard could be considered efficient. We would say that the gold standard is efficient if there is (a) a tendency for the price of gold to return to its official price, and (b) if market price of gold doesn’t different too much from the official price.

Under the assumption that multiple countries define their currency in terms of the quantity of gold, let’s consider a two country example. Suppose that the U.S. defines the dollar as 1/20 of an ounce of gold and the U.K. defines the pound as 1/4 of an ounce of gold. It follows that the price of one ounce of gold is $20 in the U.S. and £4. Note that this implies that $20 should buy £4. Thus, the exchange rate should be $5 per pound. We can use this to discuss important results.

Suppose that the current exchange rate is equal to the official exchange rate. Suppose that I borrow 1 pound at an interest rate for one period and then exchange those pounds for dollars and invest those dollars in some financial instrument in the U.S. that pays me a guaranteed rate of for one period.

The cost of my borrowing when we reach the next period is . But remember, I exchanged pounds for dollars in the first period and 1 pound purchased 5 dollars and invested these dollars. So my payoff is . I will earn a profit if I sell the dollars I received from this payoff for pounds, pay off my loan, and have money left over. In other words, consider this from the point of view in period 1. In period 1, I’m borrowing and using my borrowed funds to buy dollars and invest those dollars. In period 2, I receive a payoff in terms of dollars that I sell for pounds to pay off my loan. If there are any pounds left over, then I have made an arbitrage profit. Let denote the forward exchange rate (the exchange rate in period 2), defined as pounds per dollar. It follows that I can write my potential profit in period 2 as

We typically assume that in equilibrium, there is no such thing as a perpetual money pump (i.e. we cannot earn a positive rate of return with certainty with an initial investment of zero). This implies that in equilibrium, this scheme is not profitable. Or,

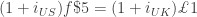
Re-arranging we get:

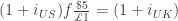
This is the standard interest parity condition. Note that is defined as pounds per dollar. If the gold standard is efficient we would expect the forward exchange rate to equal to official exchange rate (we should rationally expect that the gold market tends toward equilibrium and the official prices hold). Thus, one should expect that . Plugging this into our no-arbitrage condition implies that:

In other words, the interest rate in both countries should be the same. There is a world interest rate that is determined in international markets.

However, remember that this is an equilibrium condition. Thus, at an point in time there is no guarantee that this condition holds. In fact, in our arbitrage condition, we assumed that there are no transaction costs associated with this sort of opportunity. In addition, under the gold standard, we do not have to exchange dollars for pounds or pounds for dollars. We can exchange dollar or pounds for gold and vice versa. Thus, under the gold standard what we really care about are market prices of the same asset in terms of dollars and pounds. For example, consider a bill of exchange. The price paid for a bill of exchange is the discounted value of the face value of the bill.

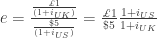
So if the ratio of the prices of these bills differ from the official exchange rate, there is a potential for arbitrage profits. As the equation above implies, this can be reflected in the ratio of interest rates. However, it can also simply be observed from the actual prices of the bills.

Officer (1986, p. 1068 – 1069) describes how this was done in practice (referencing import and export points as what we might call an absorbing barrier under which it made sense to engage in arbitrage, given the costs):

In historical fact, however, cable drafts in the pre-World War I period were dominated by demand (also called “sight”) bills as the exchange medium for gold arbitrage. Purchased at a dollar market price in New York, the bill would be redeemed at it pound face value on presentation to the British drawee, with the dollar-sterling exchange rate give by the market price/face value ratio. When this rate was greater than the (demand bill) gold export point, American arbitrageurs (or American agents of British arbitrageurs) would sell demand bills, use the dollars thereby obtained to purchase gold from the U.S. Treasury, ship the gold to London, sell it to the Bank of England, and use part of the proceeds to cover the bills on presentation, with the excess amount constituting profit.

[…]

When the demand bill exchange rate fell below the gold import point, the American arbitrageur would buy demand bills, ship them to Britain, present them to the drawees, use the proceeds to purchase gold from the Bank of England, ship the gold to the United States, and (if not purchased in the form of U.S. coin) convert it to dollars at the U.S. mint.

Thus, we can think of interest rate differentials as opportunities for arbitrage directly, or as reflecting the current market exchange rate. In either case, the potential opportunities for arbitrage profits ultimately kept gold near parity. In fact, Officer (1985, 1986) shows that gold market functioned efficiently (and in accordance with our definition of efficiency).

With this in mind, we have a couple of important questions. This discussion focuses entirely on the microeconomics of the gold standard. In subsequent posts, I will shift the discussion to macroeconomic topics.

Towards an Alchian-type Approach to Political Economy

In my previous post, I discussed what I called the sleight of hand of an Olson-approach to political economy. The basic idea of that post was that Olson’s theory of concentrated benefits and dispersed costs is often used to malign policies deemed to be inefficient. The sleight of hand aspect is as follows. First, the economist deems a particular policy to be inefficient using a standard theoretical model. Second, the economist hypothesizes that the reason we have such an inefficient policy is due to special interests getting what they want because the costs are dispersed. Third, the economist examines either in historical detail or through regression analysis the role of special interests in getting the policy implemented. Fourth, if special interests are found to have had an effect on the policy being put into place, the economist concludes that the reason we have this inefficient policy is due to special interests. However, the inefficiency of a particular policy is determined by some theoretical model. The empirical finding that special interests had a marginal effect on the policy’s implementation is then used to explain why we got this inefficient policy. Whether or not this is the correct interpretation of the empirical result depends critically on whether the theoretical assertion is true!

Let me elaborate on this point using an example. Consider the example of pollution, which is a principles of microeconomics textbook version of an externality. Suppose that in the absence of special interests, such as environmental groups, pollution would go untaxed. Empirical evidence would show that a tax on pollution was due to the influence of special interest groups (the environmental groups). If we had no concept of externalities and we used the perfectly competitive model as our benchmark model, the conclusion would be that special interests were to blame for this inefficient policy. However, since this is a commonly understood externality, one would not conclude that special interests were to blame for an inefficient policy. On the contrary, the special interest groups would be the reason for implementing the socially optimal policy. In other words, finding evidence of the role of special interest groups does not tell us anything about what is efficient or what is optimal. To do so, we need an explicit theoretical argument or model. Not only that, to come to the correct conclusion we need a correct theoretical model in the sense that it addresses relevant factors, such as externalities.

In my previous post, I criticized economists for too often simply asserting that a policy is inefficient and subsequently applying Olson’s model to explain why we get such stupid, inefficient policies. I also argued that political economy should shift to using an evolutionary argument. In that post, I was short on some of these details. As a result, in this post I want to outline what I meant by this.

In 1950, Armen Alchian published a paper entiled “Uncertainty, Evolution, and Economic Theory.” In that paper he outlines an evolutionary approach to economic theory. Specifically, he argues that it might be misleading to describe firms as profit-maximizers. The reason is that when firms face decisions, there might be a distribution of outcomes across each decision. If these distributions overlap, then it doesn’t make sense to think of the firm as maximizing anything. For example, one distribution might have a higher average profit, but also be associated with a greater variance in profit than some other possible decision. So if firms aren’t maximizing profit, what are they doing?

Alchian suggested that we think of firms as practicing trial-and-error and imitation. Firms try certain things to see what works and imitate things that worked for other firms. Along the way, some firms benefit from good luck and other firms suffer from bad luck. Nonetheless, through this process of trial-and-error, imitation, and uncertainty, the profit mechanism ultimately determines what firms are able to stay in the market and what firms must leave the market. Firms that earn a profit are able to continue operating. Firms that are losing money will be forced to drop out of the market. The profit and loss mechanism therefore selects for firms who are making a profit. This might be due to the firm’s decision-making or it might be due to luck (or some combination of the two). Nonetheless, the economist should be able to explain the success (or lack thereof) of firms. An economist can look at the characteristics and decisions shared by the surviving firms and contrast those characteristics and decisions of the firms that have left the market. In doing so, one can get the sense of the role of decision-making and luck as well as the types of decisions that have proven successful and unsuccessful.

In my view, political economy would benefit from the same sort of approach. Rather than start with a baseline model to determine whether some policy is efficient or not, one should start with the policy itself.

1. What was the primary justification for the policy? More importantly, under what grounds could we consider the policy to be efficient? These questions help to set a much more relevant benchmark than some abstract model of the economist’s choosing.

2. Once these questions have been answered, the economist has some general idea about the conditions under which the policy would be considered efficient. Now, one can take an evolutionary approach to the policy. Did the policy survive for a long time and/or is it still around? What other states or countries have adopted the same or similar policies? How did states and/or countries adopting the policy perform along the relevant dimension in comparison to others? Did any other states/countries have similar policies and abandon them? What happened if they did?

The answers to these questions help to determine the conditions under which the policy survived and the relative success of those places that implemented the policy. This can help to determine if the policy actually achieved what it was supposed to and/or whether the policy is consistent with conditions under which it could be considered efficient. In addition, if the policy seems to have been an efficient response to a particular problem, it is then possible to examine why some places got rid of it and had to bear the cost of doing so thereafter.

In short, I think that it would be useful to do something in political economy with respect to government policy today that Pete Leeson has done with policies and institutions of an earlier time and place. Leeson’s work often starts by examining some policy, law, or institution that seems completely weird, strange, or backwards. He then starts with the premise that it must have been efficient. He outlines the conditions under which the policy or institution would have been efficient and then tests that theory by examining what would have to be true for his efficiency hypothesis to be correct. This approach to political economy or public choice is clearly enlightening, judging by Leeson’s publication record. However, I notice a reticence on the part of many political economists and public choice economists to take the same approach to more recent policies and institutions. The attitude toward more modern policies and institutions seems to be that we “know” that policy X or institution Y is inefficient because economic theory tells us so. Therefore we need to explain why it exists. But how do we “know” this any more than we “know” that trial by battle was a backwards and barbaric practice of no practical use? Leeson’s work showing that trial by battle was a good way of eliciting the true value that particular claimants placed on land was actually quite efficient. So maybe we should be a bit more humble about modern policy as well.

The Sleight-of-Hand of Olson-esque Public Choice

“Long-surviving democracies could therefore hardly have been dominated by the charlatans, simpletons or crooks that economists typically portray in characterizing democratic representatives.” — Thompson and Hickson (2000)

The early days of public economics (at least as a distinct field) were essentially normative. The basic idea was that economists could use economic theory to examine market failures and devise policies that correct for those failures. A quintessential example is the case of externalities. Suppose, for example, that a particular type of production produces pollution. This cost is not limited to the firms or those working for firms. This cost affects (potentially) all members of society. The social cost of production is therefore greater than the private cost. Since firms are unlikely to internalize this social cost, they tend to produce “too much.” In order to correct for this, the economist would likely recommend taxing production at a sufficiently high level to reduce production to the socially optimum level (i.e. the level that takes into consideration both the entire cost). In this world, the economist largely plays the role of technocrat, identifying market failures and offering corrective policies.

James Buchanan, one of the pioneers of what is now called public choice theory, suggested that public economics should take a different approach. In particular, he suggested that public economics should concern itself with positive economics (i.e., an analysis of “what is” rather than “what should be”). The field of public choice recognized that the process through which policy is enacted requires the deliberate actions of politicians and other policymakers as well as voters and special interest groups.

One view of policymaking that emerged in the public choice literature is most closely identified with Mancur Olson. According to this view, the democratic process contains policymakers who are capable of supplying policy and the general public who have demands on policy. The general public will tend to form coalitions, which we might call special interest groups. As the name implies, these groups are organized around a common interest. These interest groups then go to politicians and other policymakers with their concerns and petition for policies that provide direct benefits to their group. This process tends to be effective for special interest groups because politicians are self-interested. A politician cares about getting re-elected. As such, the politician has an incentive to give the special interest groups want they want because the benefits are concentrated within the group, but the costs are dispersed throughout society. Since the costs are so small for the average voter and/or taxpayer, the marginal cost of taking action to oppose the policy exceeds the marginal benefit.

The usefulness of this theory is that it enables economists to explain the existence and persistence of inefficient policies. One shouldn’t be surprised to observe inefficient policies if those policies are providing concentrated benefits and dispersed costs. This is no doubt an insightful positive approach to the behavior of politicians and the process of policy determination.

Despite the theory’s usefulness in explaining “what is”, empirical applications of this theory often engage in a sleight-of-hand technique. For example, some public choice scholars studying a particular policy will start their analysis by using economic theory to examine a particular policy. If the policy is found to be inefficient in theory, it is natural to ask why the policy exists. One hypothesis is that this is simply an example of Olson’s theory. The public choice economist can then go back and analyze who benefits from the policy and what politician(s) supported the policy to see whether it is a simple application of concentrated benefits and dispersed costs. In the case of simple legislation, the public choice economist might even estimate a regression model of the likelihood that a particular legislator voted in favor of the policy using data on special interest influence.

The reason that I say that this application of Olson’s theory is a sleight-of-hand is as follows. This sort of analysis starts with the idea that the policy is inefficient and then empirically examines whether this is a case of special interest influence. But this is an empirical test used to justify a theoretical conclusion. In other words, economists identify a theoretical inefficiency and determine empirically that the reason the policy exists is due to the influence of special interests.

Why does this matter?

First, this approach to public choice is making a similar sort of mistake that early public economics was making. The economist starts with a theoretical model and analyzes the policy within the context of the model. If the policy is inefficient in the model, then the economist is left to explain why such an inefficient policy exists. But what if the model is wrong? What if the policy is correcting for an inefficiency that the economist ignored?

Second, this sort of empirical evidence can never tell us whether or not the policy is inefficient. In fact, it would be surprising if one didn’t find evidence of special interest influence on legislation. This is because special interests will promote their own interests, regardless of whether the policy is welfare-improving. So an economist will be likely to observe special interest influence both in cases when the special interests bring an inefficiency to the attention of policymakers and when they are just looking for a giveaway.

For a proper analysis of this Olson-based approach, economists need to develop a much better understanding of the black-box nature of the political process. The idea that special interests shape policy is not surprising. However, different political systems will select for particular policies. Countries with a given set of institutions might select for policies that appear to be inefficient, but in reality are efficient responses to some social problem previously ignored by economists. Other institutional structures might select for giveaways to special interests.

For the Olson-based approach to be useful for evaluating the efficiency properties of policy requires an evolutionary approach. Thus, the analysis of policy requires returning to the point at which the policy was adopted and attempting to identify what inefficiency the policy could possibly be aimed at eliminating. Did the policy persist and for how long? Then, one can look for whether other places adopted similar policies. If so, did the policy persist and for how long? Does the policy seem to have eliminated these inefficiencies? Among the places that didn’t adopt the policy, did they turn out better or worse in regard to this supposed inefficiency? Why did some places adopt the policies and not others? What are the institutional differences that explain what policies were selected for?

The answers to these questions seem substantially more important than the results of some probit regressions of yay or nay votes.

In Memory of John Murray

This post is a bit different than normal. Most of my posts are about the minutiae of economic theory or controversies. Today’s post is personal. All of us in academia have a number of important people who have helped us in our intellectual journey and career. I have been fortunate enough to have a number of such people in my short career. One of these people was John Murray.

I first met John as an undergraduate. At the time I was a history major, but I had started to take an interest in economics. I went to see John in his office, he being the undergraduate adviser at that time. We had not met before that day. In fact, I could not have taken more than 3 courses in economics at that time. I remember that he was delighted that I was interested in economics given that I was currently a history major. After all, John was an economic historian. When I took John’s course in economic history, it really opened my eyes to thinking about history in a completely different way. I could tell, even then, that he really enjoyed the unique perspective that economists brought to the study of history. He also had a dry sense of humor that I enjoyed.

John and I always kept in touch. When I accepted my job at the University of Mississippi, John had just accepted his position as the J. R. Hyde III Professor of Political Economy at Rhodes College. He thought that it was funny that we had accepted jobs just an hour drive from another. After we moved, I invited John down here to give seminars and he invited me up there to give a seminar. The last few years, he made a habit of coming down to Oxford to have lunch with me about twice a year. While these were technically lunches, we would often chat for a couple of hours when he would visit. We would talk about our kids and our research and he would always give me advice. We would also talk about the craziest economic theories that we thought might be correct. He also loved that I had recently taken an interest in applying modern macro to historical events. At our last lunch together in October, he was especially excited to talk about how I’d recently been given tenure and how much I had accomplished from that day I initially met him in his office.

I say this was our last lunch because John died last Tuesday. He was 58 years old.

John was not only a great mentor, but an excellent scholar. John’s work on the communes of the religious group known as the Shakers is an important work on the role of incentives in the context of particular institutional environments and should be a staple of law and economics courses. He also wrote a fascinating book on an early form of health insurance in the U.S., industrial sickness funds. He was also on the editorial board of the Journal of Economic History and Explorations in Economic History. His Google Scholar page is here. I imagine that all scholars want their work to be remembered fondly. So hopefully readers will pursue some of these links.

John was one of the most genuinely nice people that you could ever meet and he had a great laugh. He was the first person in his family to go to college and once upon a time he was a high school math teacher. Having grown up in Cincinnati, he was also a Reds fan, which I am proud to say I never held against him. His Rhodes webpage has a really great description of his life and his research in his own words, which can be found here.

The last interaction I had with John was through email a couple of weeks ago. I had sent him one of my latest papers and he told me that he was really excited to read it and discuss it. Our next lunch would have been planned for the next month or so. I wish now that I’d scheduled it sooner. I miss those lunches already. All I can hope is that John is somewhere saving me a seat for our next lunch.

The Phillips Curve and Identification Problems

Frequent readers of the blog (can you be frequent if I only write about 5 or 6 times a year?) will know that I often criticize the Phillips Curve. One counterargument that I receive to my complaints about the Phillips Curve is that my critiques are unfair because they ignore the role of countercyclical monetary policy. For example, suppose that the following two things are true:

1. The central bank responds to a positive output gap by tightening monetary policy.
2. Inflation is caused by positive output gaps.

If these two things are correct, the critics say, then you might fail to see an empirical relationship between inflation and the output gap (or even a negative relationship). However, this violates point (2) which we’ve assumed to be true. Thus, we have an identification problem. The failure to find an empirical relationship might be because countercyclical policy is masking the true underlying, structural relationship. (I could make a similar argument about the quantity theory that, for some odd reason, is not as popular as this story.)

Well, if identification is the problem, then I have a solution. During the period from 1745 to 1772, Sweden’s central bank, the Riksbank, issued an inconvertible paper money. What we would now call monetary policy was carried out through discretionary means. For example, the Hat Party, which controlled the Riksdag and the Riksbank from 1739 to 1765, expanded the bank’s balance sheet in an attempt to increase economic activity. However, while monetary policy was determined through discretion, there is no evidence whatsoever that the central bank used countercyclical policy. In fact, the Hat Party explicitly thought that monetary expansions would boost economic activity. The closest thing to a countercyclical policy occurred when the Cap Party took over and reduced the money supply in an attempt to bring down the price level. However, they did this so dramatically that any good advocate of the Phillips curve would believe that this would result in a negative output gap and deflation such that the relationship would still hold.

So, what we have here is a period of time in which the identification problem is not of any significance. As a result, we can have a horse race between the quantity theory of money and the Phillips Curve to see which is a better model of inflation.

Here is a figure from my recent working paper on the Riksbank that looks at the relationship between the supply of bank notes and the price level from 1745 – 1772. The solid line represents the best linear fit of the data. This graph seems entirely consistent with the quantity theory of money.

Now let’s look at a Phillips Curve for the same period. To do so, I construct an output gap as the percentage deviation of the natural log of real GDP per capita from its trend using the Christiano-Fitzgerald filter (the trend is computed using data from 1668 to 1772). Here is the scatterplot of the output gap and inflation.

Hmmm. There doesn’t seem to be any clear evidence of a Phillips Curve here. In fact, note that the relationship between the output gap and inflation should be positive. Yet, the best linear fit is negative (but not statistically significant). Maybe its the filter. Let’s replace the output gap with output growth (a proxy for the output gap) and see if this solves the problem.

Hmm. The Phillips Curve doesn’t seem to be there either. In fact, the slope is steeper (i.e., going in the wrong direction) and now statistically significant.

So here we have a period of time in which the central bank is using discretion to adjust the supply of bank notes and there is no role for countercyclical policy. The data is therefore immune to the sorts of identification problems we would see in the modern world. In this context, there seems to be a clear quantity theoretic relationship between the money supply and the price level. And yet, there does not appear to be any evidence of a Phillips Curve.

A Theory of Tariffs as a Method of Promoting Long-Run Free Trade

Tariffs have been in the news lately. As is typically the case, economists have come to the rescue on social media and op-ed pages to defend the idea of free trade and to discuss the dubious claims that politicians make about protectionist policies. I have no quarrels with these ardent defenses of free trade (although I would note that claims about the supposed importance of New Trade Theory and New New Trade Theory and claims about the global optimality of free trade are potentially contradictory; perhaps economists don’t like NTT or NNTT as much as they claim, but I digress). Despite my general support of free trade, I also think we should take a step back and try to understand the motivations of politicians who embark on protectionist policies. In addition, I think that we should start with the basic premise that politicians are rational (in the sense that they have some objective they want to pursue and their actions are consistent with such a pursuit) and potentially strategic actors. In doing so, we might obtain a better understanding of why politicians behave the way that they do. Once upon a time, this type of analysis was referred to as public choice economics. What follows is a short attempt to do so.

Let’s start with the following basic assumptions:

1. We will refer to the country of analysis as the Home country and a trading partner as Country X.
2. Country X has imposed trade barriers on the Home country that are costly to a particular sector in the Home country.
3. Free trade is unequivocally good and is the long-run goal of all of the politicians in the Home country (I make no assumptions about the goals of Country X).

With these assumptions in mind, I would like to make the following claim:

Given that Country X is imposing a costly trade restriction on an industry in the Home country, the politicians in the Home country would like to reduce this trade restriction. They could try to negotiate the trade restriction away. However, if the Home country does not have trade restrictions of their own that they can reduce, they do not have much to offer Country X. As a result, the Home country might impose trade restrictions on Country X. By doing so, the Home country might be able to induce Country X to reduce their trade restrictions in exchange for the Home country getting rid of its new restriction.

So what is the basis of this claim? And why would politicians do this given the assumption that I made that free trade is unequivocally good and therefore all trade restrictions are bad?

Here is my answer. Without having trade restrictions on Country X, the Home country does not have anything to bring to the bargaining table to induce Country X to reduce trade restrictions (setting aside other geopolitical bargaining). So the Home country needs to create a bargaining chip, but the bargaining chip needs to be credible. For example, one way to create a bargaining chip would be to impose trade restrictions on Country X. However, for this to be a credible threat, these restrictions have to be sufficiently costly for the Home country. In other words, politicians in the Home country have to be willing to demonstrate that the trade restrictions imposed by Country X are so costly to the Home country that the politicians are willing to punish Country X even if their own constituents are harmed in the process. By demonstrating such a commitment, they now have a bargaining chip that they can use to negotiate away trade restrictions and end up with free(r) trade in the long run. At the same time, politicians in the Home country cannot broadcast their strategy to the world because this would undermine their objective. So the politicians will likely adopt typical protectionist rhetoric to justify their position.

The problem, of course, is that this is not a foolproof plan. Once the Home country imposes trade restrictions on Country X, this could turn into a war of attrition. If the Home country is not willing to commit to these trade restrictions indefinitely, then they might eventually unilaterally remove these restrictions without any benefit. Not only that, but by doing so, Country X might now see this as evidence that they can impose additional trade restrictions on the Home country without subsequent retaliation. So make no mistake. This sort of policy can be a gamble because it requires winning a war of attrition. However, some politicians might be willing to make that gamble in order to achieve the long run benefits.

On Prediction

Suppose that you are a parent of a young child. Every night you give your child a glass of milk with their dinner. When your child is very young, they have a lid on their cup to prevent it from spilling. However, there comes a time when you let them drink without the lid. The absence of a lid presents a possible problem: spilled milk. Initially there is not much you can do to prevent milk from being spilled. However, over time, you begin to notice things that predict when the milk is going to be spilled. For example, certain placements of the cup on the table might make it more likely that the milk is spilled. Similarly, when your child reaches across the table, this also increases the likelihood of spilled milk. The fact that you are able to notice these “risk factors” means that, over time, you will be able to limit the number of times milk is spilled. You begin to move the cup away from troublesome spots before the spill. You institute a rule that the child is not allowed to reach across the table to get something they want. By doing so, the spills become less frequent. You might even get so good at predicting when the milk will spill and preventing it from happening that when it does happen, you and your spouse might argue about it. In fact, with the benefit of hindsight, one of you might say to the other “how did you not see that the milk was going to spill?”

Now suppose that there was an outside observer who studied the spilling of milk at your house. They are tasked with difficult questions: How good are you at successfully predicting when milk is spilled? Were any of your methods to prevent spilling actually successful?

In theory these don’t sound like hard questions. For example, if the observer notices that you are taking preemptive action and the spilling is becoming less frequent, then isn’t this evidence that you are doing a good job at both predicting and preventing spills? Not necessarily. Your child might be maturing and gaining more experience with drinking out of a cup with no lid and therefore less likely to spill their milk. In addition, we would need to know the counterfactual of what would have happened if you had not taken action or created a particular dinner rule for your child. In other words, we need to know whether your child would have spilled the milk if you had not taken the action that you did.

Now, let’s imagine a scenario in which the observer studying your dinner table is naive and just records what happens. Based on their observations, the observer then has to explain why the milk spills. Since the naive observer sees you take action (perhaps even frequently), but also records instances where the milk spills, the observer might come away with the conclusion that you know how to prevent spills (they see you taking such actions), but that you don’t do a good job predicting spills. Their recommendation would be that you need to get better at predicting spills.

As you have certainly realized by now, this post is not meant to be about milk or the weird person observing your dinner habits. It is really about business cycles and countercyclical policy. Naive critics of macroeconomics often point to recessions (especially severe recessions) and say “why didn’t macroeconomists see this coming?” This is an incredibly naive and silly critique in the same way that concluding that you could prevent all of your child’s spills if you were just better at prediction. This view is naive for several reasons. First, we do not have the counterfactual. What would have happened if we had done things differently? It is possible that it might have prevented what we observed, but we need to have a model of how things would have played out differently. It is also possible that there was nothing that we could do or that our actions could have made things even worse. Second, even if we live in a world in which there is some Pareto-improving policy that would have prevented the recession and everyone knows it, this doesn’t mean that we would never have recessions. In fact, in a world of a commonly known Pareto-improving policy, recessions would only occur when they were not predicted. In other words, virtually by definition, recessions would be unpredictable events in that world. To the naive observer, however, they only see the data. They do not have the counterfactuals. Thus, they are likely to conclude that macroeconomists are terrible at their jobs because they never see the recession coming. Put differently, their criticism of macroeconomics would be that macroeconomists fail to predict unpredictable events. That critique is as silly as crying over spilled milk.