On Exhaustible Resources, Part 2

Yesterday’s post on exhaustive resources has drawn a lot of ire from critics. Some have argued that I didn’t address the problem of economic growth. In short, the argument is that there are two sources of economic growth. The first is that increased efficiency of resources allows us to produce more stuff with the same amount of resources. The second is that because resources are more productive we tend to use more of them. Others have argued that algebra is irrelevant to the problem.

I’d like to address both of these concerns because they are wrong. First, let’s address the algebra issue. The model I presented in my previous post is an example of using formal economic theory to make a point that is apparently not obvious to people. If society has exhaustible resources, will markets completely deplete those resources and leave us with nothing? What the model shows is that this will not happen. It doesn’t happen because as the resource is depleted, the price of the resource rises thereby encouraging people to use less of it. (Correspondingly, if resources are near the point of depletion shouldn’t energy prices be a lot higher?) So attacking me for using algebra will get applause from a certain type of audience and “algebra doesn’t solve environmental calamity” makes a really good bumper sticker, but it is not a valid critique. The model is an exercise in maintaining consistent logic.

Now to the more substantive critique. This is the critique that growth not only comes from changes in productivity but that these changes in productivity lead to greater resource use. So let’s tackle this problem head-on using a modified version of the Solow Model.

Before going through the model let’s recall the crux of the debate:

• George Monbiot claimed that perpetual growth is not possible in a world of finite resources.
• I replied that perpetual growth comes from finding more efficient ways to use resources (the ability to produce the same amount of stuff with fewer resources).

Let’s imagine that there is an aggregate production function that is given as

where is output, is the quantity of exhaustible resources, is capital, is a parameter, is the productivity of energy use. So has the interpretation of “effective units of resources.” Now let’s assume that

where is the rate of resource extraction. Note here that I am assume no uncertainty. The amount of resources are known and declining with use.

Also, I will assume that

where is the growth rate of the productivity of energy use.

Finally, the law of motion of the capital stock is given as

where is the savings rate and is the depreciation rate on capital.

Define as effective units of resources and as capital per effective unit of resources. The corresponding law of motion for capital per effective unit of resources is given as

From this equation, there is a stable and unique steady state equilibrium for if . A sufficient condition for this to hold is .

Now, let . Note that this implies that in the steady state, . Thus, output per effective unit of resources should be constant in the steady state. This implies that the growth rate of output itself satisfies

It follows that in the steady state equilibrium, we can experience perpetual economic growth so long as the productivity of energy use rises by more than enough to offset the rate of resource extraction. Put differently, we can experience long-run economic growth even in a world of finite resources as long as we continue to use those resources more efficiently. Recall that Monbiot argued that it is impossible. I, on the other hand, argued that this is incorrect because growth is the result of being able to produce the same amount of stuff with fewer resources. This is precisely what I meant.

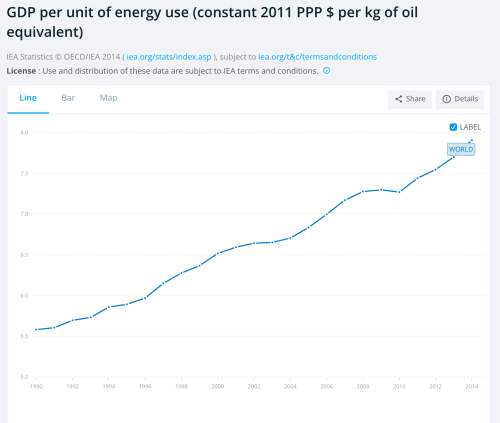
Of course, we might wonder if this is actually going on in reality. So let’s go to the data. We can measure the productivity of resource use by plotting GDP relative to energy consumption. The following figure is from the World Bank.

As one can see from the graph, there has been a considerable productivity increase in the use of energy over the last few decades. This is not the whole story since this graph only measure . One would need to compare this to to determine whether we are currently on a sustainable path. Nonetheless, the claim made by Monbiot was that perpetual growth is not possible in a world of finite resources. What I have shown is that this is wrong as a logical statement. Furthermore, my basic model in this post actually understates our ability for perpetual growth since I assumed that it is not possible to substitute from the exhaustible resource to either another exhaustible resource or to a renewable resource.